Minimum-Velocity Throw ※ veridical.net

My boy is still small and learning to catch, so I’m cautious of not throwing it too hard. As the saying goes: when you have a hammer everything looks like a constrained optimization problem, so my caution graduated into wondering what flight path angle results in the lowest possible throwing velocity that will still reach the target.

I assumed the answer would be 45°,¹ but I’ve been doing more management than math lately, so proving it became a good opportunity to stretch old muscles.²

First a diagram, which is where all problems in Newtonian mechanics should start.

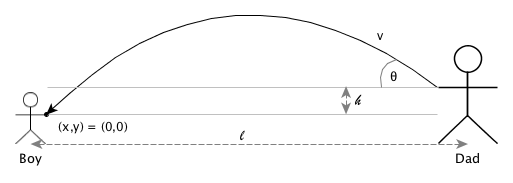
Playing catch

From this, the equations of motion for the position, $s$, as a function of time are:

$$ \begin{equation} \label{eq:s_x} s_x = - v t \cos{\theta} + l \end{equation} $$

$$ \begin{equation} \label{eq:s_y} s_y = -\frac{1}{2} g t^2 + v t \sin{\theta} + h \end{equation} $$

These equations implicitly encode the initial boundary conditions at $t=0$.³ Specifically, I release the ball at distance $l$ and height $h$ with velocity $v$ and flight path angle $\theta$.

By definition, the coordinate system origin is located where the ball is caught. Or in maths, at time $t$, $s_x = s_y = 0$.

The goal is to determine what angle $\theta$ minimizes $v$ within the constraint that the ball actually reach my son. So we need to find an equation for $v=f(\theta)$ that we can use calculus to minimize. Solving $(\ref{eq:s_x})$ for $t$ and plugging it into $(\ref{eq:s_y})$ yields:

$$ t=\frac{l}{v \cos{\theta}} $$

$$ 0 = -\frac{1}{2}g \left(\frac{l}{v \cos{\theta}}\right)^2 - v \sin{\theta} \left(\frac{l}{v \cos{\theta}}\right) + h $$

We get our function for $v$ by multiplying through by $\left(v \cos{\theta}\right)^2$:

$$ 0 = -\frac{g l^2}{2} - v^2 l \sin{\theta} \cos{\theta} + h v^2 \cos^2{\theta} $$

$$ v = -\sqrt{\frac{g l^2}{2}} \left(l \frac{\sin{2\theta}}{2} - h \cos^2{\theta} \right)^{-1/2} $$

Now some calculus. Setting the derivative $\frac{dv}{d\theta} = 0$ and solving for $\theta$ gives us the optimum flight path angle.⁴

$$ \frac{dv}{d\theta} = 0 = \frac{\sqrt{g} l}{2\sqrt{2}} \frac{\left(l \cos{2\theta} + h \sin{2\theta} \right)}{\left(l \frac{\sin{2\theta}}{2} - h \cos^2{\theta} \right)^{3/2}} $$

We assume for the moment that the mess in the denominator isn’t zero at our solution, which leave us to solve:

$$ 0 = l \cos{2\theta} + h \sin{2\theta} = \sqrt{l^2 + h^2} \sin{4\theta} $$

Since $\sin{a} = 0$ when $a = \pi$, then $\theta = \frac{\pi}{4}$, or 45°. (Quick aside: Plugging 45° back into the nasty denominator we can show our assumption is valid as long as $l \neq h$, which seems like a reasonable assumption for a game of catch.) This is unsurprising, as 45° is the answer we were expecting. Just like the max range problem from ballistics, the solution doesn’t depend on the distance between thrower and catcher or the acceleration due to gravity. It was surprising, to me at least, that the optimal angle did not depend on the difference in height, $h$⁵. This is lucky, as I won’t have to recalculate the optimal $\theta$ as my son grows up.⁶

Because it’s the solution to the maximum range ballistics problem. ↩
Also, I’ve never put any math on this site before, so now I had an excuse to install the render_math plugin and develop some LaTeX skills. ↩
They also ignore drag, the curvature of the Earth, and several other totally unnecessary complications. ↩
Yes, I know you also need to check the boundary conditions. That, as they say in textbooks, is an exercise left to the reader; although, common sense should suggest throwing the ball with no arc would require infinite velocity and throwing the ball straight up is not a solution. ↩
Or perhaps the ratio between the height and distance. ↩
Never you mind that at some point achieving a minimum velocity throw will no longer be an objective. ↩

Minimum-Velocity Throw

Published

Tags

Contact